Regularization (L1/L2) and Why Your Models Overfit
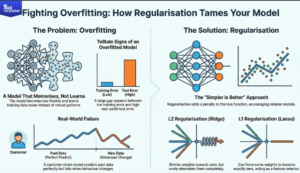
Machine learning models can be excellent when tested on the data used for training, but quite often they fail to live up to expectations when real-world data are used. The reason for this gap is mostly overfitting: the model ends up learning noise and idiosyncrasies rather than general patterns. Regularization (L1/L2) may be a rather modest in appearance, but a very effective method for keeping models under control and for improving generalization.
What is overfitting in practice?
Overfitting is a situation where a model is so flexible relative to the number and the quality of data that it starts to memorize training examples instead of learning robust rules. Typical indicators of overfitting are: very low training error coupled with much higher validation/test error, predictions that are not stable, and the model being sensitive to small data changes.
As an instance, a complex model used for predicting customer churn might perfectly follow every tiny fluctuation of the past behavior but when the customer behavior changes even a bit it can fail terribly.
How regularization helps
Regularization imposes a penalty on large weights in the loss function, thus it encourages simpler models which do not depend heavily on any particular feature. The concept is: “If a slightly less perfect fit on the training data leads to a more robust model on new data, then this should be preferred.”
L2 regularization (Ridge) imposes a penalty that is proportional to the square of the weights. It usually moves weights toward zero in a smooth manner but hardly ever makes them exactly zero.
L1 regularization (Lasso) imposes a penalty that is proportional to the absolute value of the weights. Through that, some weights can be completely zeroed thus feature selection is implicitly done.


