Your dataset might have hundreds of features, but both humans and simple models struggle in high, spaces. Techniques for Dimensionality Reduction such as PCA and t-SNE can help you to compress the data into 2, 3 dimensions for visualization, quicker model training, and better insights.
Connect With Us: WhatsApp
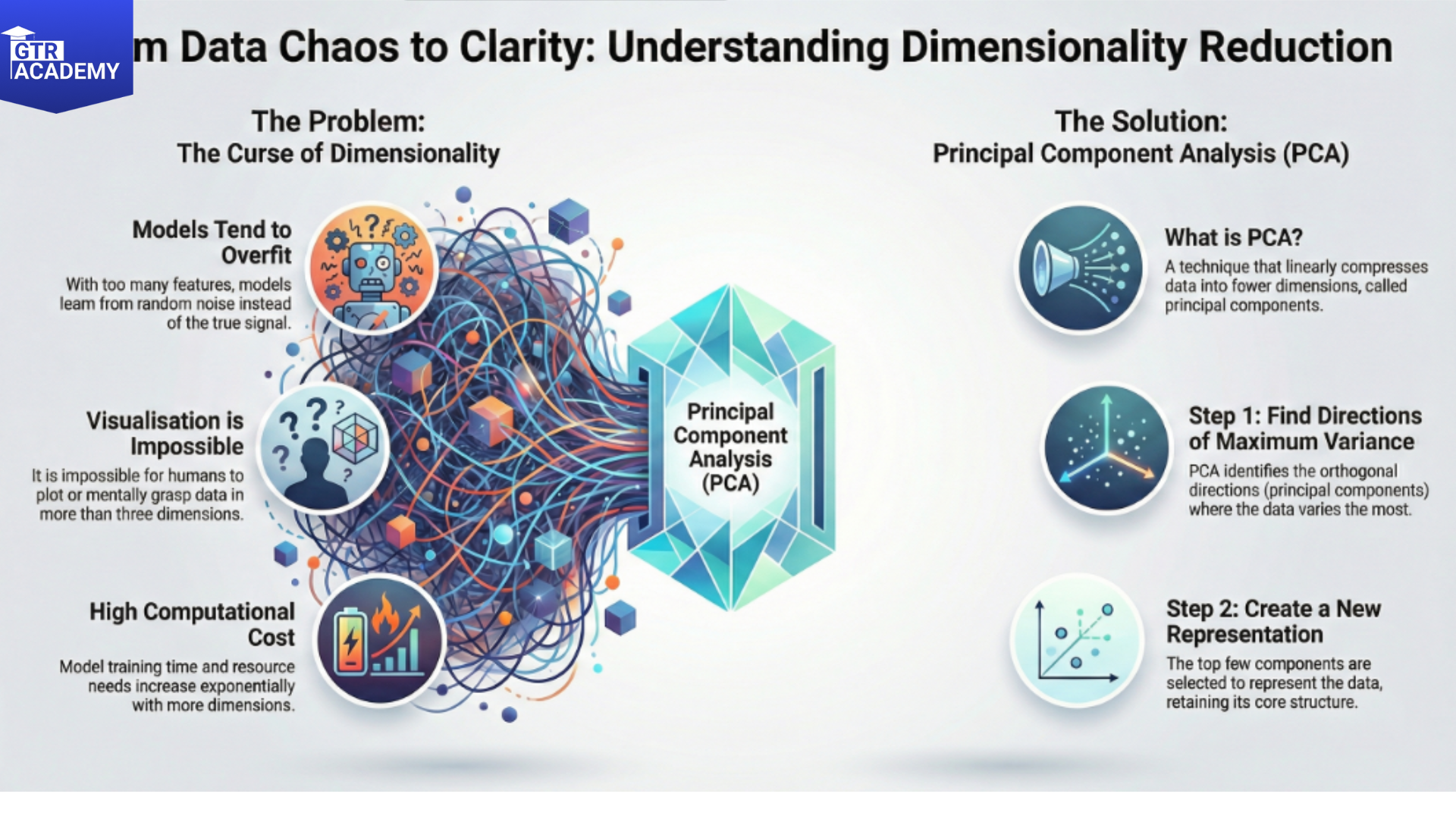
The curse of dimensionality
Problems with high-D data:
- The curse of dimensionality: Distance measurements lose their meaning; most of the space is empty.
- Overfitting: The model learns noise instead of signal.
- Visualization: It is impossible to plot or grasp 100+ dimensions.
- Compute cost: Training goes exponentially slower.
Dimensionality methods seek a low, dimensional representation that retains as much of the relevant structure as possible.
PCA: Linear compression to maximum variance
- Principal Component Analysis (PCA) identifies orthogonal directions (principal components) that account for the most variance:
- Subtract the mean from the data. Determine the covariance matrix. Extract eigenvectors (directions with the greatest variance) and eigenvalues (quantity of variance). Top k components are used to represent the data.
Advantages:
It is linear, quick, and the components are easily interpretable as they are linear combinations of the original variables. Removal of noise and decorrelation.
Examples:
- Use PCA as a step in preparing data for modelling.
- Analyze and visualize groups of customers or sensor data.
- t-SNE: Nonlinear for visualization
- t-Distributed Stochastic Neighbor Embedding (t, SNE) is remarkable for 2D/3D visualization:
- Transforms high D distances into similarities.
Maps to low D space preserving local structure (similar items stay close). Uses t distribution in low D to avoid crowding problem.
Advantages:
- It makes visible to the human eye clusters as well as manifolds.
Limitations:
- It is not deterministic (random seed has an impact). Very slow on big data sets.
- It modifies the global structure of the data (it is better to use it just for data exploration, not for measuring distances).
Practical example: customer segmentation
Here is the workflow:
- text
- Raw data: 50 features (demographics, behavior, purchases)
- → PCA: top 3 components explain 85% variance
- → Plot PC1 vs PC2 → clear clusters emerge
- → t-SNE on same data → even crisper separation for viz
- → Use clusters to stratify models or target campaigns
- When and how to use them
Checklist for readers:
- PCA before modelling if (features >> samples) or high correlation.
- t‑SNE/UMAP for EDA and cluster discovery (sample first!).
- Always validate low‑D viz should align with business intuition.
Try this: Take a customer or product dataset with 20+ features. Run PCA to plot top 2 components. Do you see patterns that match known segments?
Subscribe for daily tools and patterns data teams live by!
Connect With Us: WhatsApp
